Packing them in

How can n points be distributed on a circle such that they maximize the minimum distance between any pair of points?

Of course! Don’t be daft, this is easy!

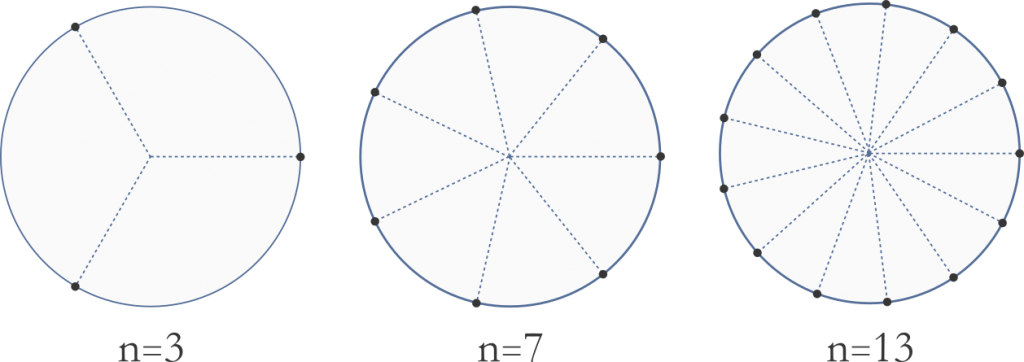
So far so primary school! Next!

How can n points be distributed on a sphere such that they maximize the minimum distance between any pair of points?

I… Errr… I think…. I… Erm… Can’t be that hard!?

Actually it all gets a bit tricky - the problem having given both Plato and Euler some sleepless nights. As a result of this pondering I now have a new favourite contemporary mathematician, Neil Sloane, who rather brilliantly has devoted a reasonable chunk of life to looking at this. He maintains a set of tables with all known solutions. Reading around this (and the related Thomson Problem) gave me an idea - can we create weird bounding geometry based upon Professor Sloane’s spherical packing codes?

Demo

Presenting the (lets be honest - rather less than useful and not very catchily titled) Turtlestack NX Custom Feature - the ‘N Face Bounder’…

Frankly, you are more likely to want a bounding box or convex hull generated against your geometry, which NX can already do! That said I think there might be a role for this in generating packable shapes to encompass irregular forms? Perhaps if you chose the packing arrangement which would lead to a Platonic solid when bounding a sphere you might get nice stackable forms even for ‘irregular’ contents?